PSYC 2530: Information Processing
And metaphorical mechanisms
Matthew J. C. Crump
Last compiled 03/29/22
Reminders
Reading is Chapter 7 on Information Processing
Grades
Discussion Boards
Roadmap
1 Revolutions and Metaphors
2 Donders and Processing stages
3 Information Theory
4 Hick-Hyman Law
Metaphors and explanation
Cognitive psychology often uses metaphors as an aid for explanation
Metaphorical Explanation
The structure and function of one thing is used to roughly describe another thing
Revolutions and metaphors
Big metaphors in cognition roughly track technological revolutions
- Industrial Revolution
- Technological Revolution
- Digital Revolution
Industrial Revolution
Cognition is like a factory assembly line

Technological Revolution
Cognition is like a telephone network

Digital Revolution
Cognition is like a computer

Roadmap
1 Revolutions and Metaphors
2 Donders and Processing stages
3 Information Theory
4 Hick-Hyman Law
Mental Chronometry
Using measures of time to make inferences about cognitive processes

How fast can a nerve transmit a signal?
Infinitely fast?
Or, with a certain speed?
Hermann von Helmholtz (1821-1894)
Measured nerve conduction speeds in sciatic nerve of a frog
Range of 24.6 - 38.4 meters per second

FC Donders (1818-1889)
Dutch Ophthalmologist
Used mental chronometry to measure mental processing times

Physiological Reaction time
First used in astronomy
Referred to individual human error in the timing of recording observations of stars
Time taken for light to hit the eye, then be transduced and conducted along nerves to produce a response

Donders’ idea
The time associated with unique stages of mental processing could be measured by systematically asking people to complete tasks of increasing complexity…
Donders’ Tasks
Donders measured reaction times in increasingly complex tasks
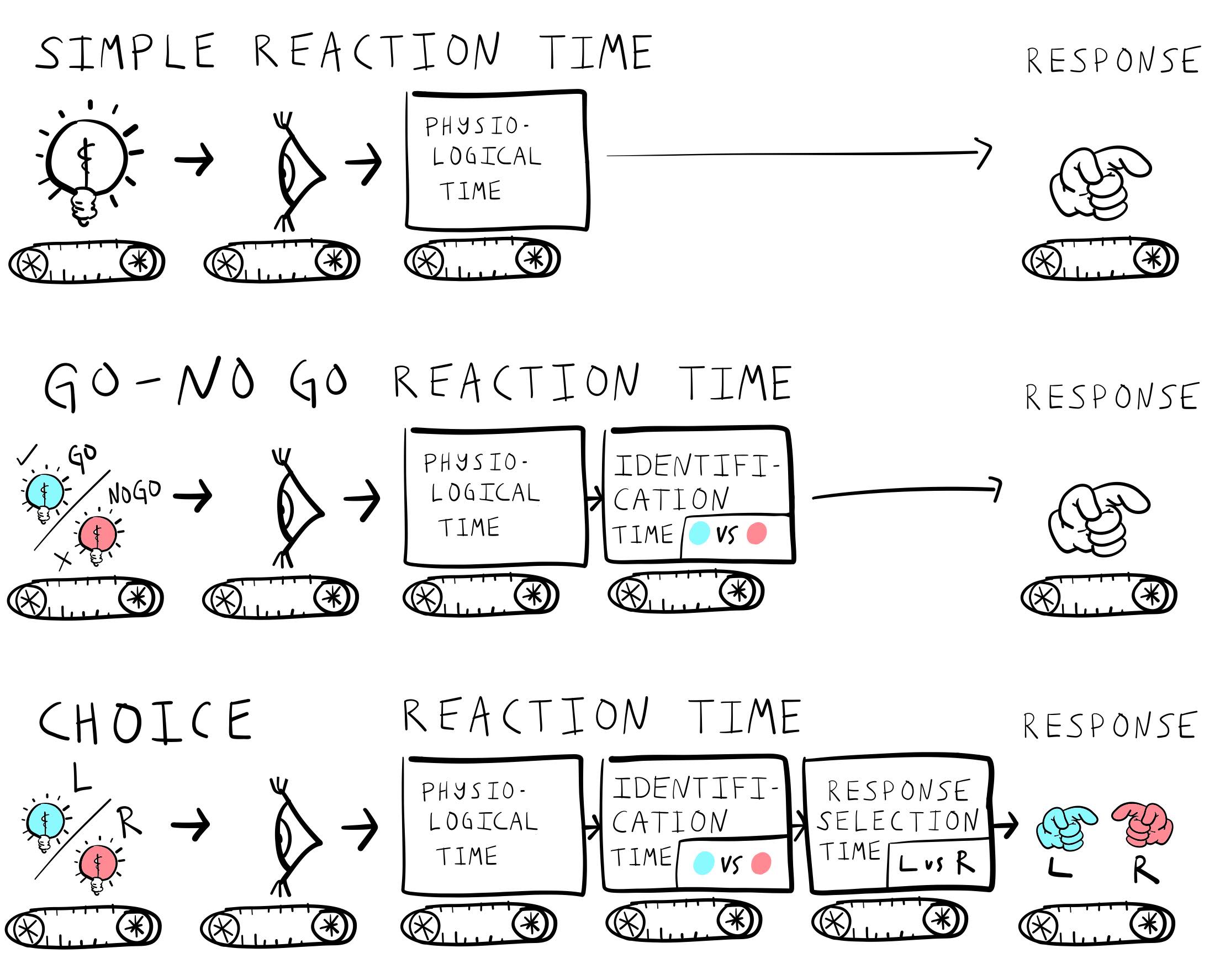
Simple reaction time
Go-No Go
Choice reaction time
Simple Reaction Time
Simplest reaction time task
Participants wait for ANY stimulus
And, respond as quickly as possible when the stimulus occurs
Measures “physiological” reaction time
Go-No Go
Participants wait for a specific stimulus (GO)
Respond only to the GO stimulus
Withhold response to other stimuli
Requires stimulus identification
Choice Reaction Time
There are multiple possible stimuli
Respond to each with a unique response
stimulus identification and response selection
Donder’s processing stages
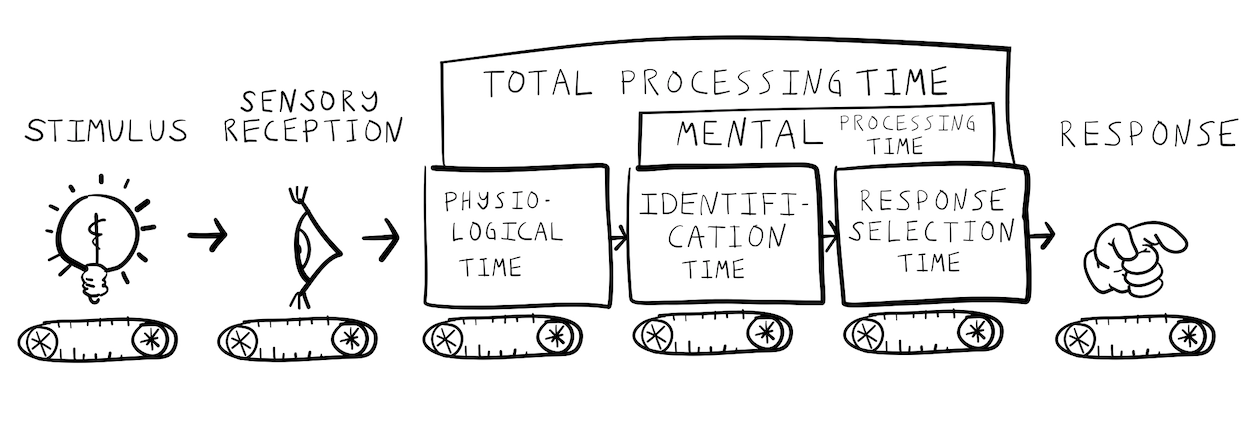
Assumed mental times
Donders subtractive logic
Estimating identification time
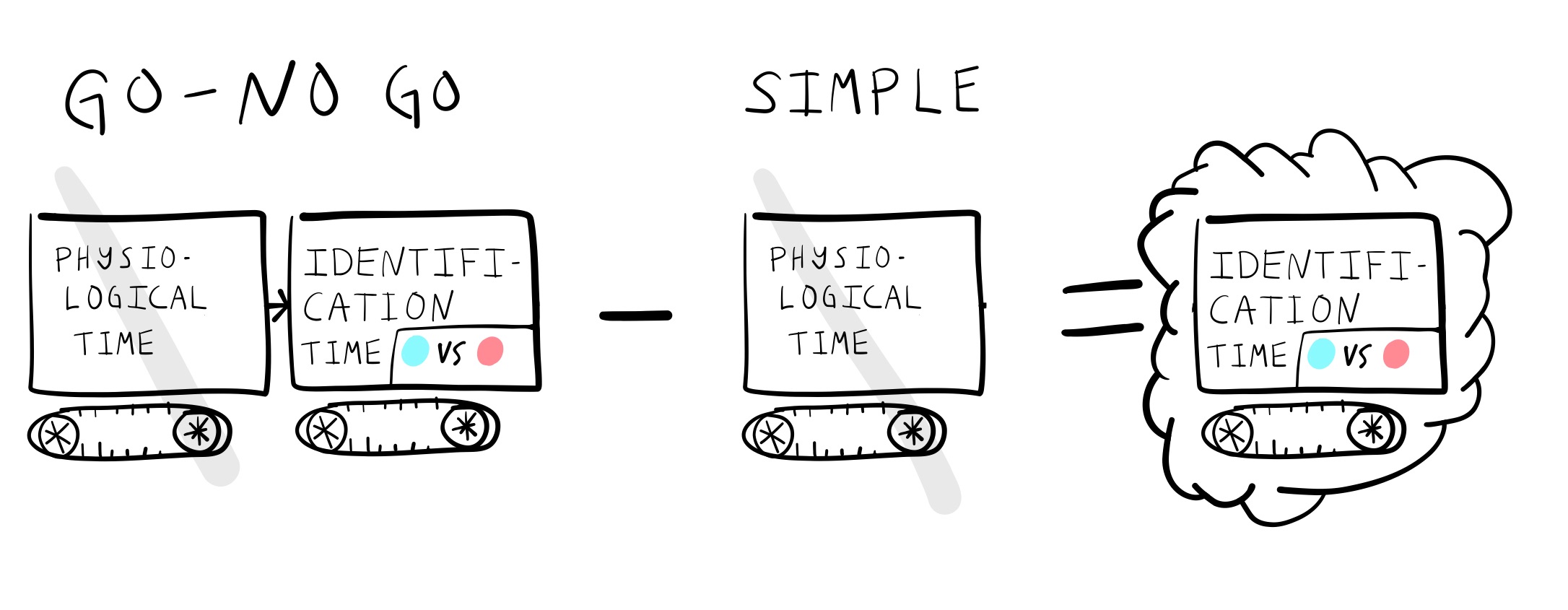
Donders subtractive logic
Estimating response selection time
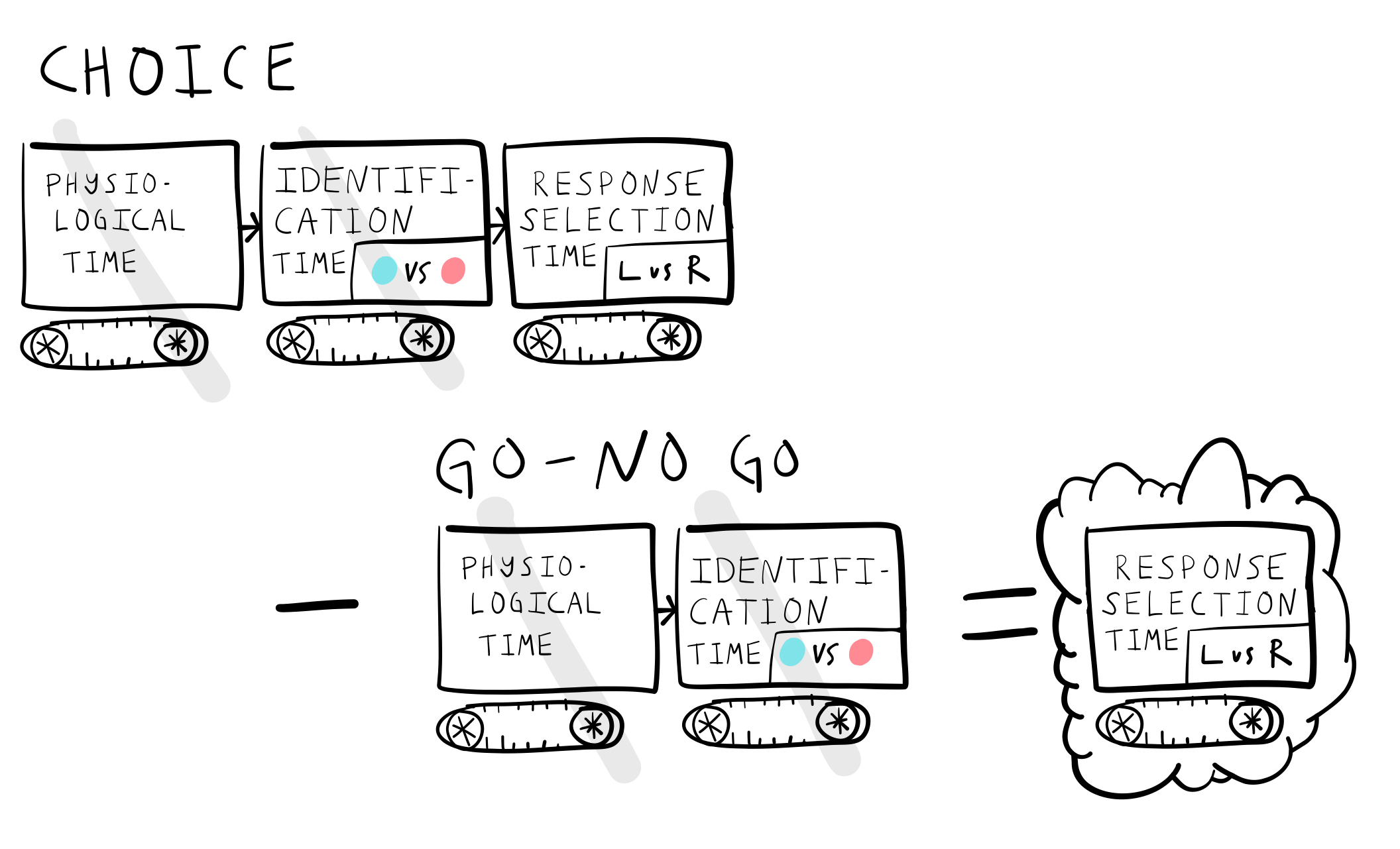
Issues with subtractive logic
What happens if two processing stages can both occur in parallel at the same time?
1950s and beyond
Interest in reaction time studies was revived in the 1950s
And, the metaphor for explaining cognitive processes shifts from an assembly line metaphor to a telecommunications metaphor
PRP effect
PRP stands for the Psychological Refractory Period (Welford, 1952)
Theoretical debate about the PRP effect reflects the metaphorical shift
Basic PRP effect
Responding to a first stimulus can sometimes delay a response to a second stimulus, especially if the stimuli are presented quickly, one after the other
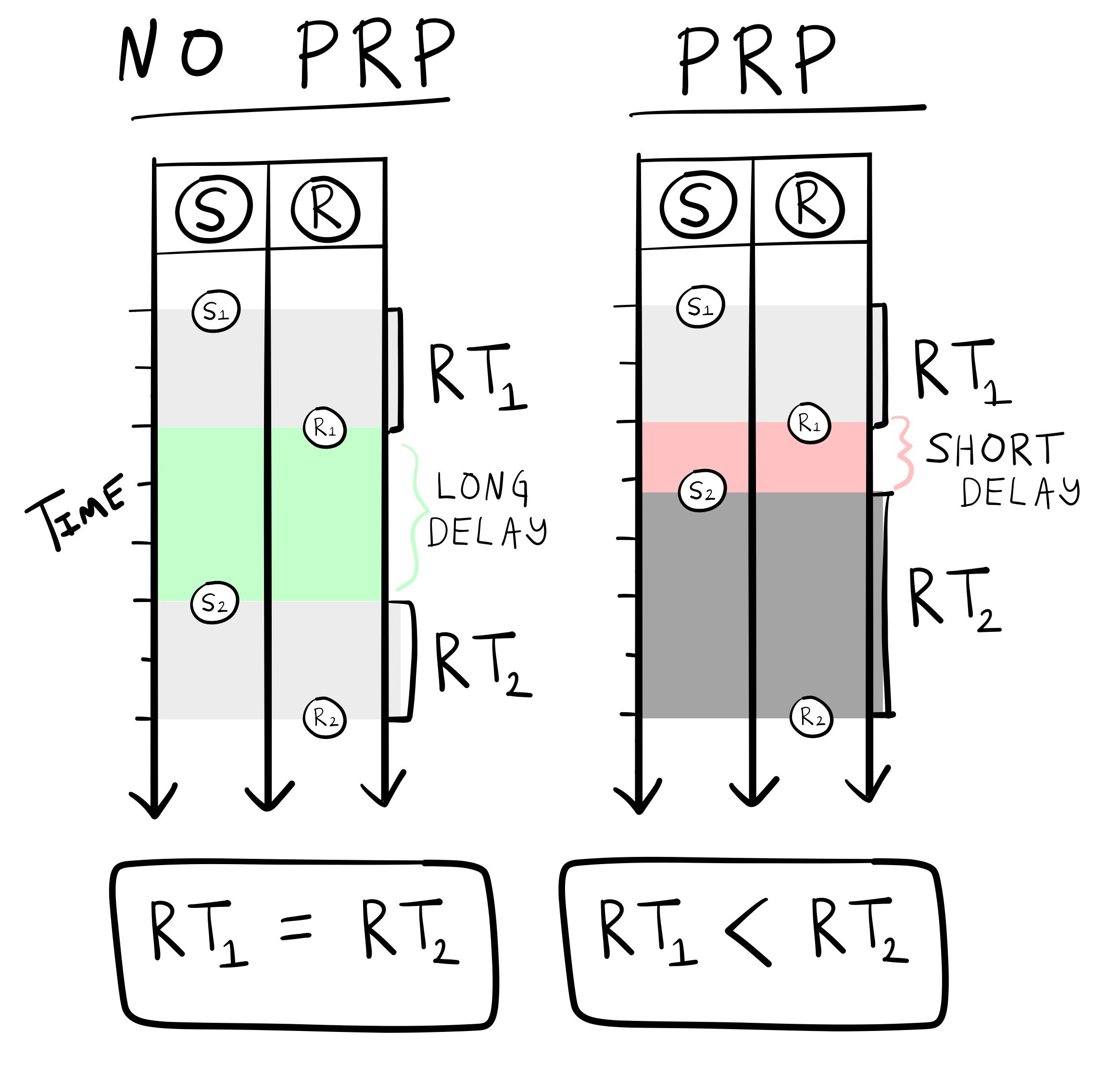
Explanations of the PRP effect
Welford described a few:
- Could reflect hard-wired properties of signalling among nerve fibers
- Could reflect participants expectations…short delays might be more surprising, and the surprise lengthens the response
- PRP reflects a central mechanism with a single-channel of limited capacity…
A single channel decision mechanism
In its bare essentials this theory assumes, firstly, a number of sensory input mechanisms each capable of receiving data and storing it for a limited period so that, for example, a short series of signals can be received as a unit. Secondly, it assumes a number of effector mechanisms containing both central and peripheral elements and capable of carrying out a series of actions such as the pressing and release of a key or a series of taps (Vince, 1949) as a single unit. Thirdly, between these two it postulates a single-channel decision mechanism. This is regarded as being of limited capacity in the sense that it takes a finite time to process information and can thus only deal with a limited amount of information in a given time
Roadmap
1 Revolutions and Metaphors
2 Donders and Processing stages
3 Information Theory
4 Hick-Hyman Law
Claude Shannon (1916-2001)
“Father of Information Theory”
A Mathematical Theory of Communication (1948)
Founded digital circuit theory (1937)

Information theory intro
Information theory was NOT originally developed as a theory in psychology
It is a set of mathematical formalisms to describe communication systems
Measurement tools from information theory became popular in Cognitive Psychology beginning around 1950
Information Channel
An information channel has three parts:
A sender, a channel, and a receiver
Two questions:
How much information was sent?
How much was received?
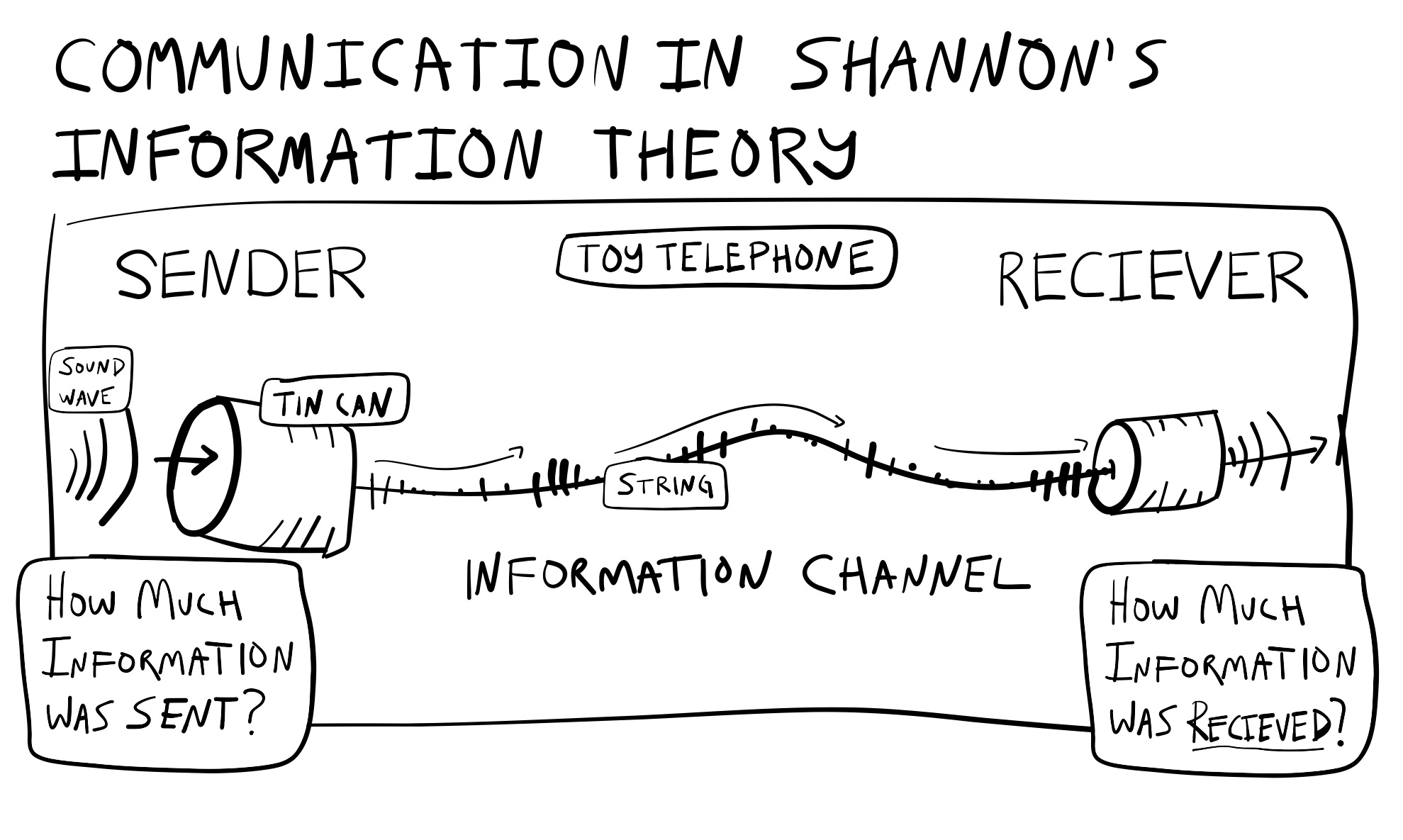
Example information channels
Toy telephone (two cans and a wire)
Real telephone networks
What about people talking to each other?
Channel Capacity
Important concept from information theory
The amount of information that can be transmitted and received through a communication channel
Measuring information: H
Shannon proposed to measure information in terms of entropy, or the amount of uncertainty in a system of messages:
\(H(X) = -1*\sum_\text{i=1}^n P(x_i) * log_2 P(x_i)\)
Why a formula is useful
Capacity limitations for information channels could be measured and assigned a value
Content of signals could be analyzed in terms of how much information they carry
Amount of information lost during transmission could be quantified
Led to improvements in telecommunications systems and technology
Meaning of H?
Shannon’s formula defines information in terms of the predictability of a sequence of messages.
More predictable sequences = Low information
Less predictable sequences = High information
Consider three books
A book that contained the letter A repeatedly
A book that you read, enjoyed, and found meaningful
A book that contained completely random sequences of letters
Computing H
https://www.crumplab.com/cognition/textbook/information-processing.html#computing-h
Bits of information
Shannon’s formula uses a base 2 logarithm which produces a number in the unit of bits.
Bits can be used to measure the total number of discrete events in a system of messages
Bits and Unique events
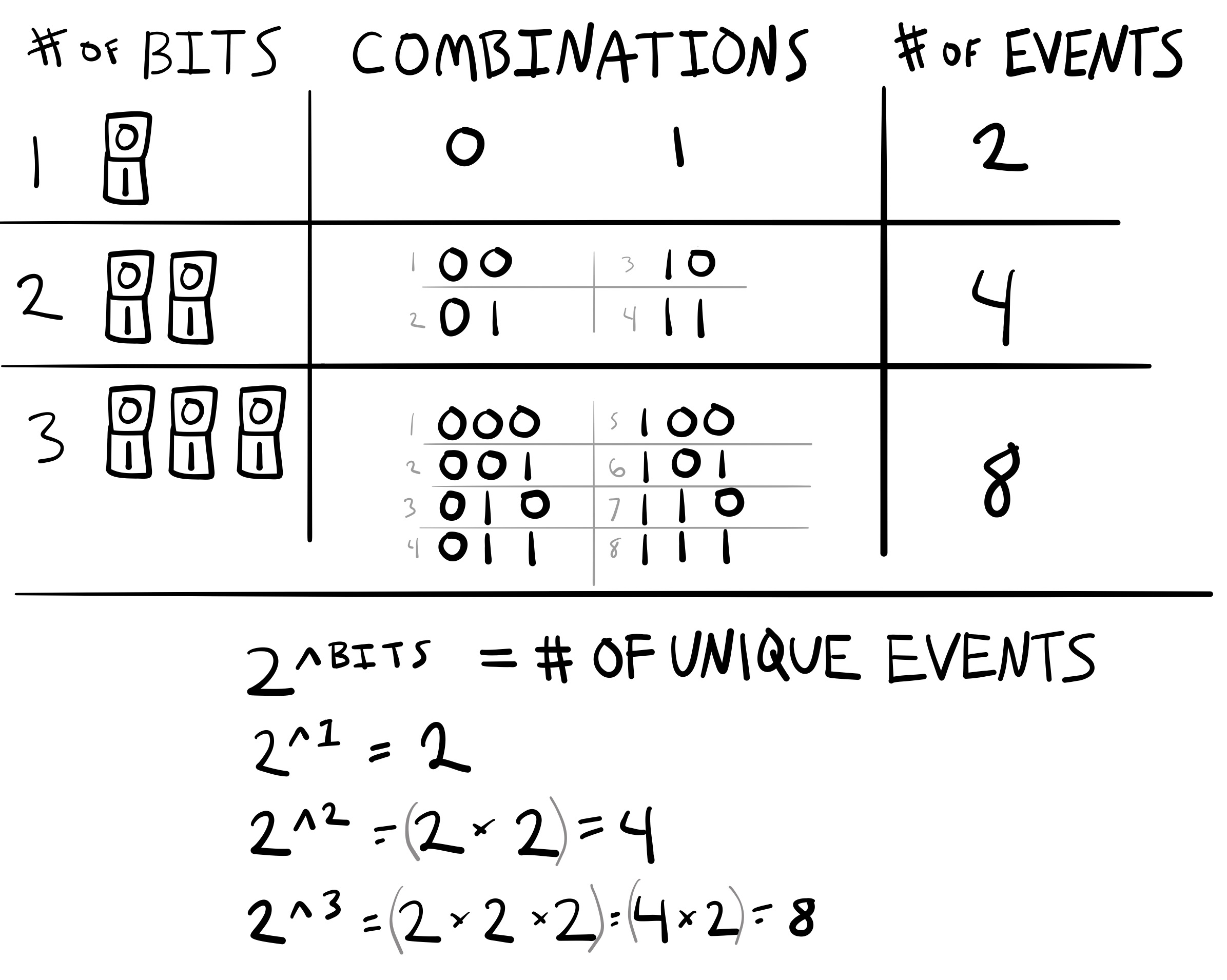
A simple communication system
Let’s review H, Bits, and Information together by examining a simple communication system involving four possible messages:
A B C D
Roadmap
1 Revolutions and Metaphors
2 Donders and Processing stages
3 Information Theory
4 Hick-Hyman Law
Information theory and cognition
Ideas from information theory were imported into cognitive psychology around the 1950s
Information processing capacity
A big idea was to describe limitations in “information processing” abilities
E.g., how much “information” can you process?
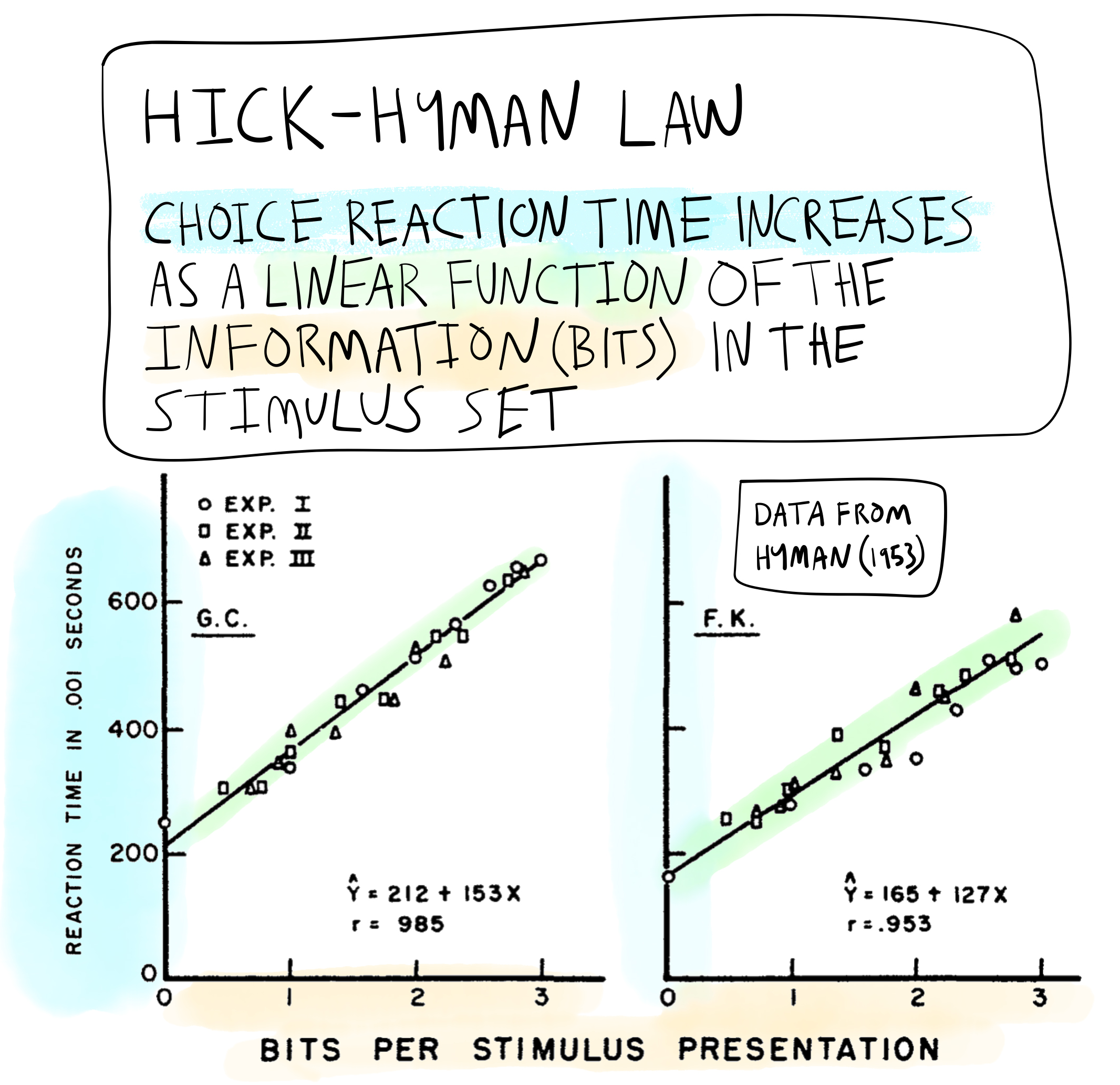
Hick-Hyman Law
A promising early demonstration suggesting that choice reaction time performance may be fundamentally governed by the amount of information in a set of choice stimuli.
Specifically, choice reaction time increases a linear function of the information in the set of choice stimuli.
Choice Reaction Time Task
Participants are presented with one stimulus at a time from a set of stimuli
Participants identify each stimuli with a unique response as fast as possible

Set-size effects
Prior research had shown that choice reaction time increases with set-size
e.g., average response time to respond to any stimulus goes up and up, as the number of alternatives in the set increases
Explaining set-size effects…
Why does mean reaction time go up when the number of possible choices goes up?
Hick and Hyman’s idea
Perhaps people were responding to the amount of information in the choice set, and not simply the number of the alternatives.
If people were responding to the amount information, then they should be sensitive to the predictability of individual alternatives.
Confounds
Choice stimuli were usually presented randomly to participants.
This meant the number of alternatives and the amount of information in a set was confounded.
Deconfounding alternatives and information
Need to independently manipulate the number of alternatives, and the amount of information
Hyman (1953)
Hyman, R. (1953). Stimulus information as a determinant of reaction time. Journal of Experimental Psychology, 45(3), 188–196. https://doi.org/cq3kjd
Experiment 1
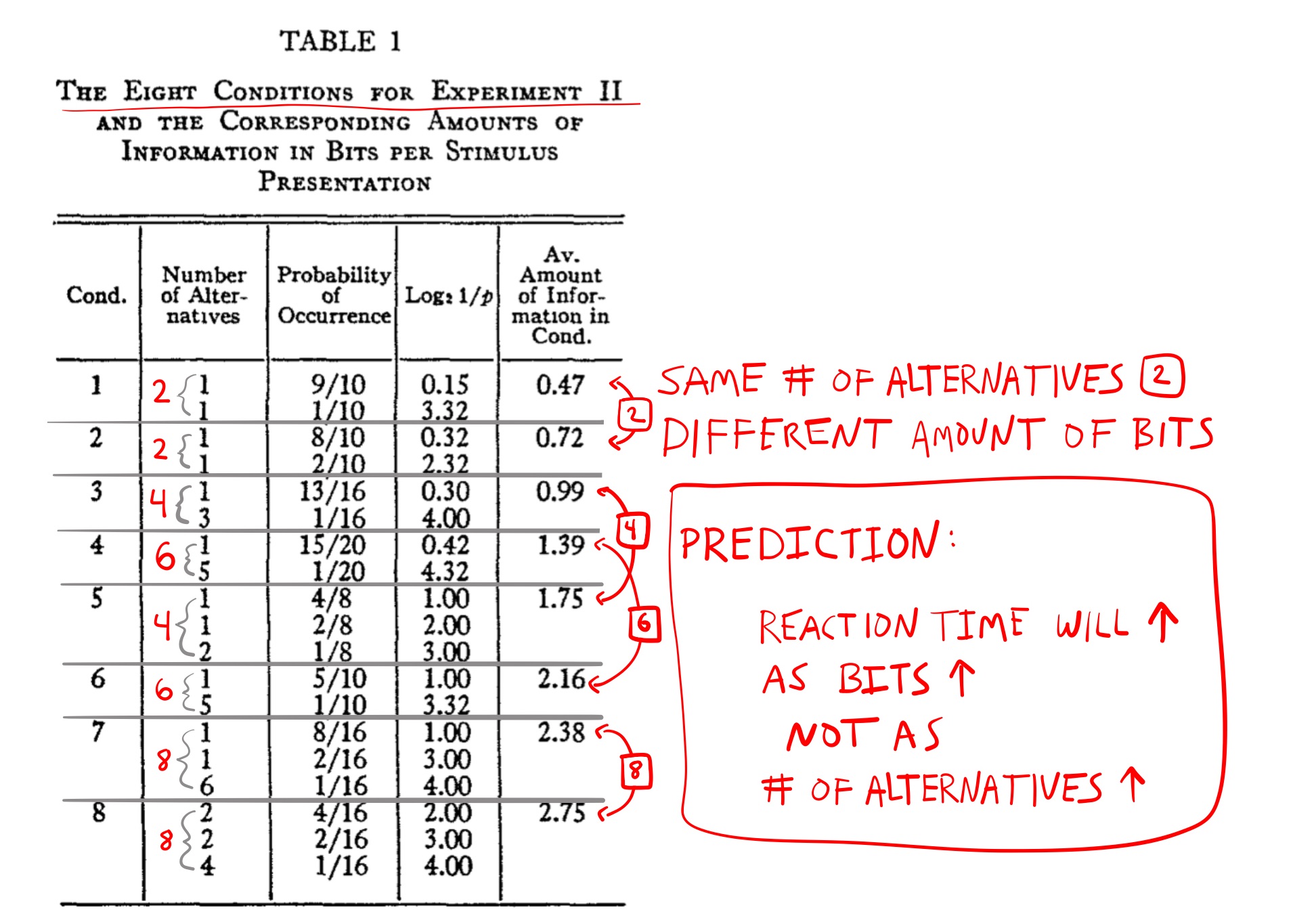
A choice-reaction time task with 8 different conditions, corresponding to the number of alternatives in a set, from 1 to 8.
In each condition, all stimuli were presented randomly.
Thus, the amount of bits in each condition was ranged from 0 to 3 (bits for 1 to 8 alternatives are: 0, 1, 1.58, 2, 2,32, 2,58, 2,81, and 3).
Experiment 1 results
Reaction time increased linearly with number of alternatives…
BUT, the number of alternatives, was completely confounded with the amount of bits.
Experiment II
Results
Hick-Hyman Law
Choice reaction time increases linearly as a function of the information (bits) in the stimulus set
Implications for Behaviorism
Behaviorists looked for lawful regularities connecting a stimulus with a subsequent response
Hick-Hyman law showed a case where responses to a stimulus did not depend on the stimulus that was presented!
People were not only responding to the stimulus in front of them, their performance was also determined by the relative predictability of other stimuli that were not presented.
Debate about Hick-Hyman Law
Information theory was not an explanation, it was just another way to describe the experimental manipulation
Further research showed some violations to the Hick-Hyman Law (practiced subjects, non-linear trends)
Explanations
Why does choice reaction time mostly increase linearly as a function of information?
Hick’s match to template hypothesis…
Hick’s binary logic test hypothesis…
Kornblum’s priming explanations
What’s next
Complete the quiz for this learning module on Blackboard, and/or the writing assignments by the due date.
The next learning learning module is Memory I